Définition de la symétrie centrale - Séquence complète : 1ere Secondaire

Séquence complète sur “Définition de la symétrie centrale” pour la 1ere Secondaire

Notions sur “La symétrie centrale”

Cours sur “Définition de la symétrie centrale” pour la 1ere Secondaire

Deux figures symétriques par rapport à un point O sont deux figures qui se superposent par un demi-tour autour de ce point O.

Le point autour duquel on fait un demi-tour s’appelle le centre de symétrie.

Une symétrie centrale de centre O est donc un demi-tour autour du point O.

La transformation qui transforme A en A’ est une symétrie centrale.
Effectuer une symétrie centrale c’est effectuer un demi-tour autour d’un point.

Le point A’ est le symétrique du point A par rapport au point O si le point O est le milieu du segment [AA’].
Le symétrique du point O par rapport au point O est le point O lui-même

La phrase « O est le milieu du segment [AB] » a la même signification que « le point A est le symétrique du point B par rapport au point O » ou alors
« Le point B est le symétrique du point A par rapport au point O ».

Dans la figure précédente, on peut aussi dire aussi que A est le symétrique de A’ par rapport à O.

Attention à ne pas faire la confusion entre symétrie centrale et symétrie axiale.

« A′ est le symétrique de A par rapport à O » (symétrie centrale car O est un point).

« A’ est le symétrique de A par rapport à (d) » (symétrie axiale car (d) est une droite).

Exercices avec correction sur “Définition de la symétrie centrale” pour la 1ere Secondaire

Consignes pour ces exercices :

Compléter les phrases suivantes sur le modèle de la première phrase :

Observer la figure suivante. Il s’agit d’un labyrinthe.

Observer la figure ci-contre :

Observer la figure suivante :

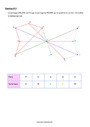
Entourer en rouge le dessin qui représente la figure et sa symétrique par rapport au point représenté.

Traduire la phrase codée en remplaçant chaque lettre par son symétrique par rapport au point X.

1. Compléter les phrases suivantes sur le modèle de la première phrase :

• M’est le symétrique de M par rapport à O signifie que O est le milieu du segment [MM’].

• B est le symétrique de A par rapport à O signifie que …… est le milieu du segment ……

• F est le symétrique de E par rapport à A signifie que …… est le milieu du segment ……

• J est le symétrique de M par rapport à O signifie que …… est le milieu du segment ……

• …… est le symétrique de …… par rapport à …… signifie que A est le milieu du segment [BC].

• …… est le symétrique de …… par rapport à …… signifie que O est le milieu du segment [MN].

• …… est le symétrique de A par rapport à …… signifie que T est le milieu du segment [AA’].

• …… est le symétrique de …… par rapport à …… signifie que G est le milieu du segment [EF].

• …… est le symétrique de …… par rapport à …… signifie que L est le milieu du segment [IK].

Evaluation, bilan, contrôle avec la correction pour la 1ere Secondaire : Définition de la symétrie centrale

Compétences évaluées
Comprendre la définition de la symétrie centrale
Reconnaitre le symétrique d’un point par rapport à un point
Reconnaitre deux figures symétriques par rapport à un point

Consignes pour cette évaluation :

Exercice N°1

Compléter les phrases suivantes :

Deux figures sont symétriques par rapport à un point O si elles se…………. lorsque on effectue un …………. autour du ………….

Le point O s’appelle le ………

Le point A’ est le symétrique du point A par rapport au point O si le point O ……

Le symétrique du point O par rapport au point O est ……………

Exercice N°2

Compléter les phrases suivantes puis illustrer chacune d’elles par une figure tracée à main levée et codée :

Le point A’ est le symétrique du point A par rapport à O revient à dire que …. est le milieu du segment [……].
Le point R est le milieu du segment [IE] revient à dire que …. et …. sont symétriques par rapport à ….
Le point …. est l’image du point T dans la symétrie de centre F revient à dire que …. est le milieu du segment [C…].
Le segment [L…] a pour milieu le point …. revient à dire que le point M est le symétrique du point …. par rapport à N
La symétrie centrale de centre G transforme …. en O revient à dire que …. est le milieu du segment [R…].